The Role of Probability in Decision-Making: A Blackjack Case Study
- Alex Ricciardi
- Nov 29, 2024
- 7 min read
This article examines the concept of probability as a tool for quantifying uncertainty and making informed decisions, using the game of Blackjack as an example. By applying probability principles such as conditional probability, dependency, and Bayes' Theorem, it demonstrates how mathematical methods can evaluate risks, predict outcomes, and guide strategic choices in uncertain scenarios.
Alexander S. Ricciardi
November 17, 2024

Uncertainty, by definition, is a nebulous concept; it encapsulates the unknowns and ambiguities. Probability plays a crucial role in quantifying uncertainty, helping establish degrees of belief –percentages– in the likelihood of an outcome or outcomes in a given scenario or set of scenarios. This paper explores the concept of probability by applying it to a easy to understand example involving the game of Blackjack.
Probability
Probability is the likelihood of something happening. It can also be defined as a mathematical method used to study randomness. In other words, probability is a mathematical method that deals with the chance of an event occurring (Illowsky et al., 2020). This section describes some of the fundamental concepts of probability. Starting with the concept of sample space, often donated Ω. It is the set of all possible outcomes from a scenario or a set of scenarios. An event denoted E or ω is a subset of the sample space, it consists of one outcome or multiple outcomes. In probability theory, the probability of a specific possible outcome donated P(E), from the sample space is a value between 0 and 1, inclusive (Russell &Norvig, 2021). With a ‘0’ probability meaning the outcome will never occur, a ‘1’ probability meaning the outcome will always occur, and a value between ‘0’ and ‘1’ meaning the likelihood of the outcome, the higher values the greater likelihood. This can be formulated as follows:
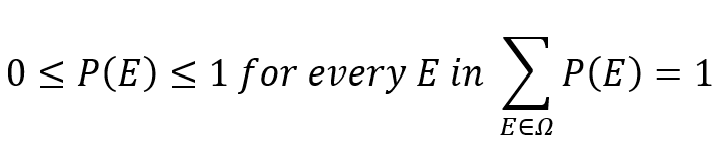
and
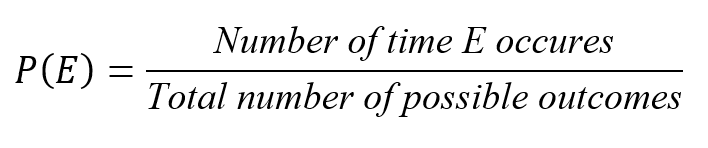
The probability method comes with a set of rules, proprieties, laws, and theorems that are fundamental principles used for computing the likelihood of events occurring. Below is a list of some of these rules, proprieties, principles, and theorems:
A and B are events.
- Addition rule: Computes the probability of either one of two events from occurring (Data Science Discovery, n.d.).
For mutually exclusive events (events that cannot occur simultaneously):
P(A ∪ B) = P(A ∨ B) = P(A) + P(B)
For non-mutually exclusive events:
P(A ∪ B) = P(A ∨ B) = P(A) + P(B) - P(A ∧ B)
- Multiplication rule: Computes “the joint probability of multiple events occurring together using known probabilities of those events individually” (Foster, n.d., p.1).
For independent events (the occurrence of one does not affect the other):
P(A ∩ B) = P(A ∧ B) = P(A) ∙ P(B)
For dependent events:(the occurrence of one does affect the other)
P(A ∩ B) = P(A ∧ B) = P(A) ⋅ P(B|A)
P(B|A): conditional probability (see below).
- Complement rule: “The complement of an event is the probability that the event does not occur” (Elberly College of Science, n,d., Section 2.1.3.2.4).
P(¬A) = 1 - P(A)
- Conditional probability: It is the probability of an event occurring given that another event has already occurred. The probability of A given B:
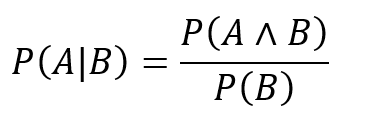
- The Bayes’ Theorem: Computes the reverse of the conditional probability. It updates the probability of an outcome based on new evidence. It can also be defined as
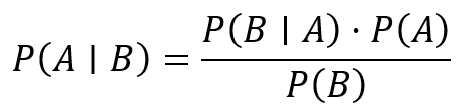
Where:
P(A) is the prior probability of an event A.
P(B) is the probability of an event B.
P(B|A) is the probability of an event B occurring given that A has occurred.
P(A|B) is the probability of an event A occurring given that B has occurred.
(Dziak, 2024)
These rules, proprieties, principles, and theorems provide a range of tools to solve probabilistic problems in simple scenarios such as rolling dice and card games like Blackjack.
Blackjack Scenario
Let's explore a Blackjack scenario when the dealer is showing a 10. In Blackjack, specific rules dictate when to take a hit or stand, especially when the dealer is showing a 10, that is the house hand is showing a 10. Suppose a single deck is in play, and four cards are already dealt. If you have a 10 and a 7 visible, and the dealer shows a 10, let's calculate the probability that the dealer's hidden card is an 8, 9, or a face card, and why it makes sense to hit on a 16 but to stand on a 17.
In this Blackjack scenario, the concepts of dependency and conditional probability play an essential role in calculating the probabilities. Two events are said to be dependent if the outcome of one event affects the probability of the other. In this scenario, the events are dependent because the cards are drawn without replacement being placed. This means that each card dealt to the player or the house hands changes the composition of the deck and thus affects the probabilities of future events.
Analyses of the Scenario
Now that the probability methods have been established let’s analyze the problem in more detail. In blackjack, the goal of a player is to finish the game with a higher hand than that of the house, without exceeding 21, as going over 21 is known as ‘busting’ and it is an automatic loss (Master Traditional Games, n.d.). The face cards have a value of 10 and Ace can either be treated as 1 or 11 with the player choosing the value. The player and the house can either hit or stand, the player or players go first, and after all the players stand the house goes next. Note that all players are playing against the house, not each other, and if the house’s hand matches a player’s hand it results in a draw between the player and the house. A standard deck of cards has 52 cards. The player's hand has a 10 and a 7, totaling 17. The house has a 10 as the dealer up-card, and a fourth card is on the table, the dealer hole-card. Therefore 3 card values are known and 52-3=49 cards are unknown. The scenario calls to calculate the probability of the house's other card, the dealer hole-card, being an 8, 9, or face card, as any of those cards would give to house a better hand than the player. A standard deck has 4 8s, 4 9s, 4 Jacks, 4 Queens, and 4 Kings. Mathematically, this can be translated to:
4(8s) + 4(9s) + 4(Jacks) + 4(Queens) + 4(Kings) = 20 house favorable cards.
This means that from a set of 49 unknown cards 20 of those cards are favorable to the house. Thus, the probability that the house's other card, the dealer hole-card, is one of the house's favorable cards is:

This means that the probability of the house having a better hand than the player is 40.82% when considering only the 8, 9, or face cards as the possible cards on the table.
On a side note, the Ace card was not considered in this scenario, and an Ace can be treated as a 1 or 11. If the dealer hole card is Ace then the house’s hand would be 10 + 11 = 21, Blackjack. A card deck has 4 Aces, additionally, the 2 remaining 10 cards were also not considered in this scenario, this changes the number of house favorable cards to
20 + 4(Aces) + 2(10) = 26 and the probability to:

This considerably improves the probability of the house having a better hand than the player from 40.82% to 53.06%.
Why It Makes Sense to Hit on a 16 but Stand on a 17?
The scenario claims that it makes sense to hit on a 16 but to stand on a 17; if the house will stand on a 17 and above. Let’s explore the scenario where the player has a hand of 16. If the player decides to hit, they can improve their hand by drawing a 1 (Ace), 2, 3, 4, or 5, that is a total of 5 types of cards out of a set of 13 types of cards (Ace through King) are favorable to the player with a hand of 16. Note that this calculation is not based on the number of cards in a deck but on the number of types of cards found in a deck, 13, rather than the total number of cards left in the deck, as the specific card composition of the player’s hand of 16 is unknown. Therefore, the probability of the player hitting a favorable type of card is:

Thus, if the house’s hand is a 17 and above, it makes sense for the player to hit as they have an approximately 38.46% chance to draw a favorable card. If the player does not hit, they will automatically lose since the house has a better hand.
Now let’s explore the scenario where the player has a hand of 17. If the player decides to stand, they can improve their hand by drawing a 1 (Ace), 2, 3, or 4, a total of 4 types of cards out of set of 13 types of cards are favorable to the player with a hand of 17. Therefore, the probability of the player hitting a favorable card is:

This means that a house with a hand of 17 above has a 69.77% and above chance of hitting an unfavorable card and bursting out. Thus, if the house’s hand is 17 or above, it makes sense for the player to stand, as the house has approximately a 69.77% or higher chance of drawing an unfavorable card and busting if it decides to hit. This is likely because the house typically plays against multiple players who may have better hands than the house.
Conclusion
Probability plays a crucial role in quantifying uncertainty; it helps establish the likelihood of an outcome or outcomes in a given scenario or set of scenarios. This paper explored the concept of probability, by applying its principles to a practical example, the game of Blackjack. This simple example shows how powerful the concept of probability can be; by demonstrating how probability can be used to evaluate risks, calculate potential outcomes, and make strategic choices. Probability as a tool for making decisions, can be apply not only in games but also in various real-world situations where uncertainty is a factor.
References:
Data Science Discovery (n.d.). Multi-event probability: Addition rule. University of Illinois at
Urbana-Champaign (UIUC). https://discovery.cs.illinois.edu/learn/Prediction-and-Probability/Multi-event-Probability-Addition-Rule/#Addition-Rule-Formula
Dziak M. Bayes’ theorem. Salem Press Encyclopedia of Science. 2024. Accessed November 18, 2024. https://search.ebscohost.com/login.aspx?direct=true&AuthType=ip,uid&db=ers&AN=89142582&site=eds-live
Elberly College of Science (n.d.). 2: Describing data, part 1. STAT 200: Elementary statistics. Department of Statistics, PennState Elberly College of Science. https://online.stat.psu.edu/stat200/lesson/2/2.1/2.1.3/2.1.3.2/2.1.3.2.4
Foster, J. (n.d.). Multiplication rule for calculating probabilities. Statistics By Jim. https://statisticsbyjim.com/probability/multiplication-rule-calculating-probabilities/
Illowsky, B., Dean, S., Birmajer, D., Blount, B., Einsohn, M., Helmreich, J., Kenyon, L., Lee, S., &
Taub J. (2020, March 27) 1.1 Definitions of statistics, probability, and key terms. Statistics. OpenStax. https://openstax.org/books/statistics/pages/preface
Master Traditional Games (n.d.) The rules of Blackjack, Master of the Games. https://www.mastersofgames.com/rules/blackjack-rules.htm?srsltid=AfmBOoojETz5j0oD9X_OW-mIYhepbOfCZm3sH6Z4o2klRDmMLHYO6s5m
Russell, S. & Norvig, P. (2021). 12.2 Basic probability notation. Artificial intelligence: A modern approach. 4th edition. Pearson Education, Inc. ISBN: 9780134610993; eISBN: 9780134671932.





Comments